Somas cruzadas
Efectuar
actividades de ludicidade matemática envolvendo números posicionados em
formas geométricas. Desta
vez, a figura escolhida engloba dois triângulos com um vértice comum:
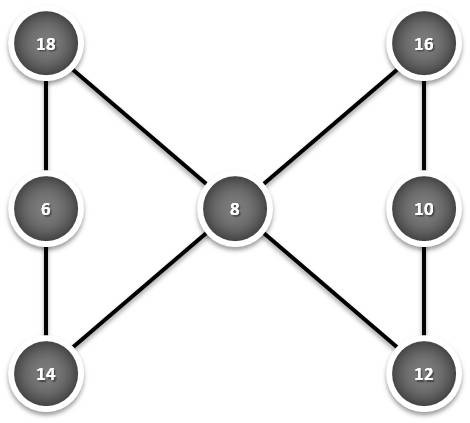
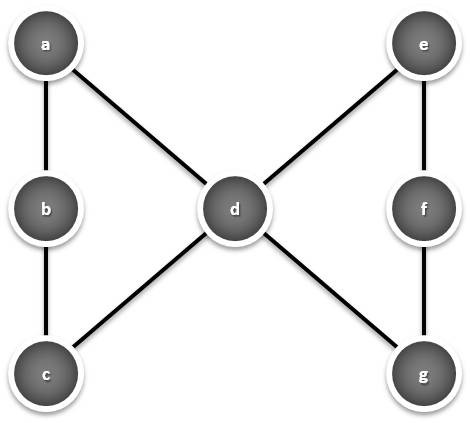
A
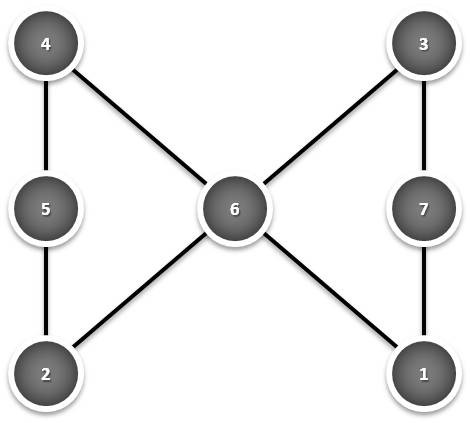
tarefa consiste em posicionar os primeiros sete números naturais, todos
e apenas uma vez, no lugar das letras, de modo que: (a + b + c = a + d +
g = e + f + g = c + d + e.
Ora
bem, as condições do enunciado da tarefa levam a concluir que a soma
dos quatro números pertencentes a cada triângulo terá de ser a mesma,
isto é: a + b + c + d = d + e + f +g. Por outro lado, a soma dos sete
valores envolvidos na tarefa é 28, pois 28 = 1 + 2 + 3 + 4 + 5 + 6 + 7.
Logo, se se excluir o valor comum (d), a soma dos seis números restantes
terá de ser um valor par, para que possibilite duas metades inteiras de
igual valor numérico, pois a + b + c = e + f + g. Sendo assim, existem
três possibilidades de isso ocorrer:
- atribuir à letra "d" o valor 2, resultando uma soma 26, subdividida em duas somas de valor 13;
- atribuir à letra "d" o valor 4, resultando uma soma 24, subdividida em duas somas de valor 12;
- atribuir à letra "d" o valor 6, resultando uma soma 22, subdividida em duas somas de valor 11.
Resta, agora, testar se para cada caso os seis números sobrantes se dividem exactamente nas duas somas de igual valor numérico:
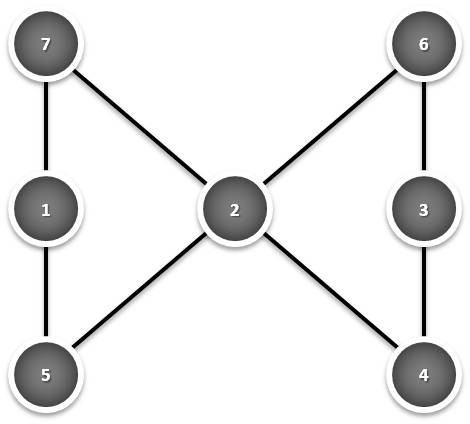
- 1º caso: 13 = 7 + 5 + 1 e 13 = 6 + 4 + 3;
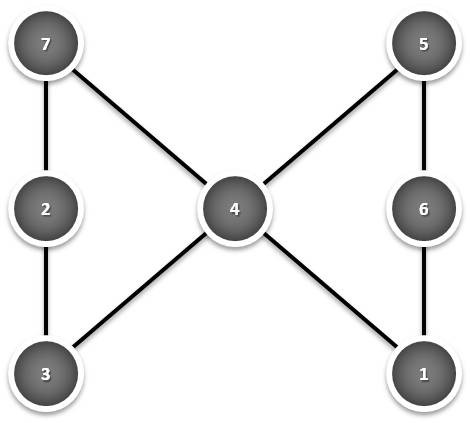
- 2º caso: 12 = 7 + 3 + 2 e 12 = 6 + 5 + 1;
- 3º caso: 11 = 7 + 3 + 2 e 11 = 5 + 4 + 2.
Testemos cada caso na respectiva figura:
1º caso:
Verifica-se, pois que 7 + 1 + 5 = 7 + 2 + 4 = 5 + 2 + 6 = 6 + 3 + 4 = 13.
2º caso:
Neste caso, confirma-se que: 7 + 2 + 3 = 7 + 4 + 1 = 3 + 4 + 5 = 5 + 6 + 1 =12.
3º caso:
Veja-se que neste caso: 4 + 5 + 2 = 4 + 6 + 1 = 2 + 6 + 3 = 3 + 7 + 1= 11.
A tarefa revelou, pois, uma natureza aberta, por permitir mais do que uma solução.
Imagine-se,
agora, um estudo envolvendo os sete primeiros múltiplos naturais do 5
e, de seguida, os sete primeiros múltiplos naturais do 10. Como se
posicionariam os números no caso de ser possível obedecer às premissas
da tarefa inicial?
Eis
uma possível solução, tirando partido, por exemplo, da ordem posicional
dos elementos envolvidos no 1º caso da tarefa inicial deste artigo:
| Múltiplos do 5: | Múltiplos do 10: |
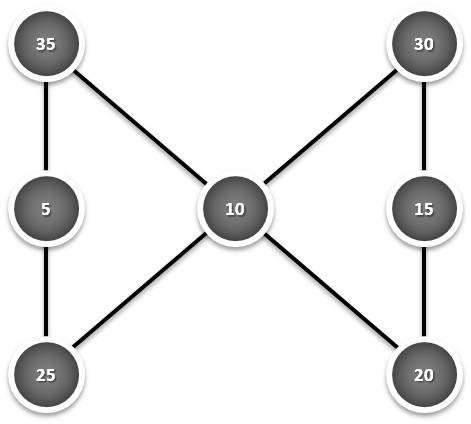 |
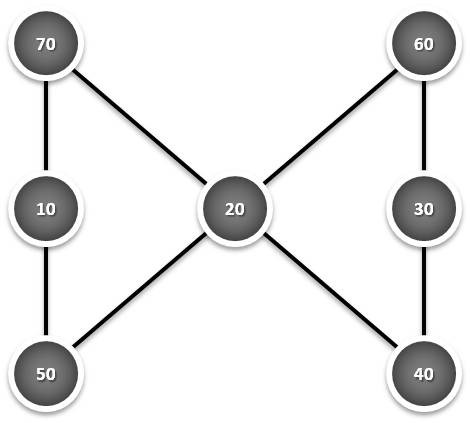 |
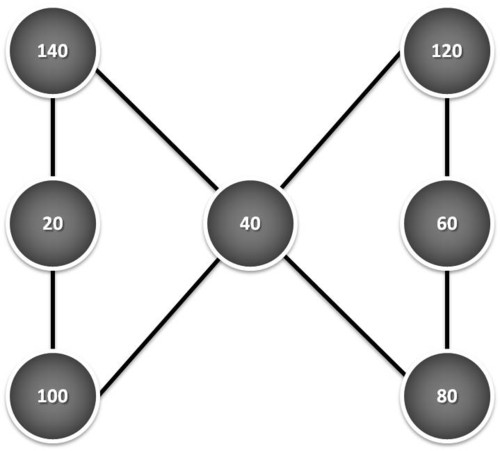
Note-se que a soma em qualquer linha da figura da esquerda é sempre 65 e nas da direita é sempre o seu dobro: 130.
Em
contexto de sala de aula, seria desejável que os alunos conseguissem
estabelecer uma relação entre o menor dos números envolvidos e a soma
mágica a obter. Note-se que a iniciar em 5, e com os múltiplos naturais
do 5, a soma foi 65; a iniciar em 10, e com os múltiplos naturais do
10, a soma foi 130, ou seja 65 + 1 x 65. Qual será a soma quando se inicia no valor 20, usando os sete primeiros múltiplos naturais deste valor?
Ora,
seria desejável que os alunos inferissem a lei geral que permite obter
uma qualquer soma (s) a partir dos sete primeiros múltiplos de números,
que sejam múltiplos naturais do cinco. Assim, s = 65 + (n - 1) x 65,
sendo "n" o número de ordem, múltiplo natural do 5. Logo, para n = 20
estaremos na presença do quarto múltiplo natural do 5 e a soma respectiva será a seguinte: s = 65 + (4 - 1) x 65 = 65 + 3 x 65 = 260. Confirmemos com a figura:
Analise
em conjunto as três figuras seguintes, encontre uma lei geral que
descreva matematicamente a soma obtida em função do respectivo menor
valor envolvido em cada uma delas e projecte a possível soma de uma nova
figura como estas, iniciada pelo valor 20:
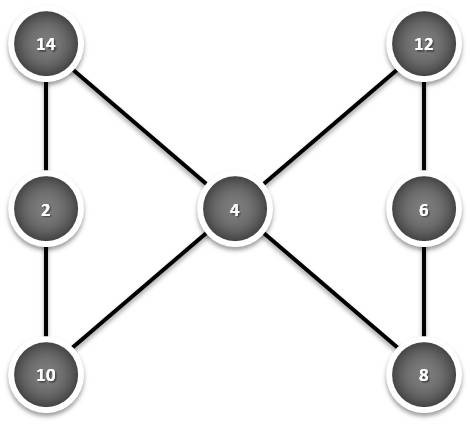 |
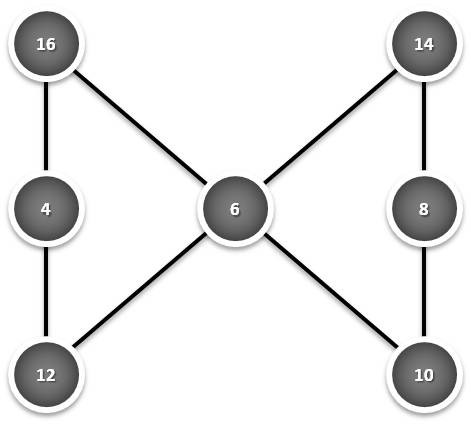 |
 |
palavras-chave: figuras mágicas, matemática recreativa, múltiplos, paulo afonso, progressão aritmética
Postado por Ramalho Vasconcelos
Fonte: Blog de Matemática Recreativa

Nenhum comentário:
Postar um comentário